《The Mathematics of Poker》中文翻译

我们也可以考虑事件A给予事件B的条件概率，也就是在事件A发生的条件下，事件B也同时发生的概率。两个相关事件A与B同时发生的概率是事件A发生的概率乘以B给予A的条件概率。如果事件A与事件B是独立的，那么A给予B的条件概率就等于事件A发生的概率。

接下来我们用具体的等式描述以上概念：

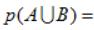事件A与事件B至少发生一个的概率；

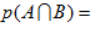事件A与事件B同时发生的概率；

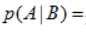在事件B发生的条件下事件A发生的概率；

那么对于两个互斥的事件就有：

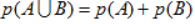； （1）

对于两个独立的事件就有：

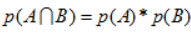； （2）

对于任意两个事件都有：

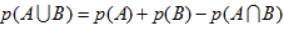； （3）

对两个相关事件有：

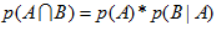；（4）

我们可以注意到式（1）就是式（3）的特殊情况（给定条件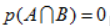即可）；同样地，式（2）是式（3）的一个特殊情况（当A与B独立时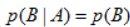，），另外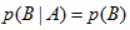可以推出p(A|B)=p(A)。

现在我们重新回到之前的问题，即起始手牌是一对A的概率到底是多少呢？观察这两个事件：

A：第一张牌是一张A；

B：第二张牌也是一张A。

我们容易知道p(A)=p(B)=1/13。然而这两个事件显然是相关的，因为当你第一张牌拿到的是A时，显然你第二张牌仍然是A的概率减小了。因此我们不能直接将这两个事件的概率相乘得到他们的联合概率，而需要计算p(B|A)。这并不难计算，在第一张牌是A的情况下，剩下的51张牌中有3张A，于是p(B|A)=3/51=1/17。

那么我们就可以轻松地得到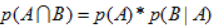=1/13*1/17=1/221。

也就是说起手牌是一对A的概率是1/221。