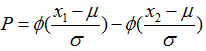《The Mathematics of Poker》中文翻译

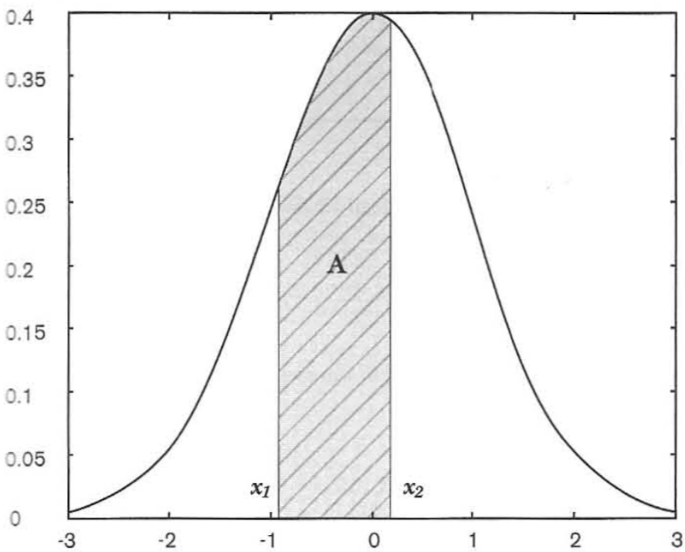
正态分布是曲线峰值在总体平均值处的铃型曲线,并且当x取值趋向于负无穷或正无穷时曲线渐进趋向于0。曲线与x轴围成的图形的面积(与所有概率分布一样)为1,而取值在[x1,x2]之间的概率就是曲线与x轴、x=x1,x=x2,围城的图形的面积,如下图中的A区域。
用不是那么正式的语句表述的话,中心极限定理告诉了我们,当你有一些总体并且有足够大的样本数量时(具体多大取决于数据的类型),样本的输出都会遵从这样均值与方差和真实均值、方差接近的铃型曲线。
给出均值 与标准差
与标准差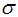 的正态分布的方程为:
的正态分布的方程为:

求出正态分布曲线中两点之间的面积可以帮助我们求出给定均值与方差的样本取值在两点之间的概率。正态分布是关于均值对称的,因此一半的区域在均值左侧,一半的区域在右侧。一个常用的计算曲线两点之间区域面积的方法叫z值法,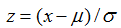 。z值代表了x值远离了多少个标准差的均值。
。z值代表了x值远离了多少个标准差的均值。
我们可以为z值找到一个叫累积正态分布函数的东西,来表达曲线下z值左侧区域的面积(均值为0、标准差为1的正态分布曲线)。我们称这个方差为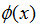 。如下图。
。如下图。

如果z是一个标准化z值,那么z的累积分布函数就是:
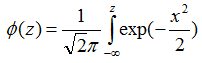
求出x1与x2之间面积的方法就是先相应求出z1和z2,并求出累积正态分布值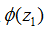 和
和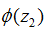 并将其相减。
并将其相减。
如果 是z值的累积正态分布函数,那么一个均值为
是z值的累积正态分布函数,那么一个均值为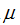 标准差为
标准差为 的正态分布函数的样本的取值落在x1与x2之间的概率是:
的正态分布函数的样本的取值落在x1与x2之间的概率是: