《The Mathematics of Poker》中文翻译

一个更极端的例子：一个职业牌手曾经告诉过本书的一个作者说他做过一个关于AK与AQ翻牌前全下的记录表格，经过一个月的线上的记录共累积到了2000个样本，两组牌的输赢比例居然接近50对50。

如果假设网站的发牌系统是完全随机的，并且双方在翻牌前不能得到任何附加信息的话，这个事件发生的可能性有多少呢？

首先我们考虑单次实验的方差或者标准差：

AK与AQ全下的胜率为73.5（考虑到所有同花或不同花的情况）。现在以1代表AK赢，0代表AQ赢。那么我们的均值就是0.735。

接下来计算方差：

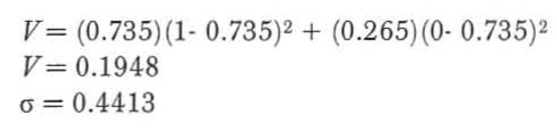
2000手牌的均值是：

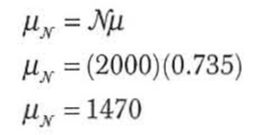
那么2000手牌的标准差是：

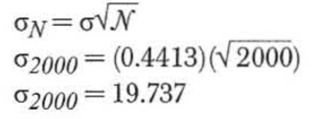
实验的结果大约是2000的50%，也就是1000，而均值是1470，那么我们就可以算出z值：

实验的结果是1000，而预期的平均结果是1470，也就是说实验的结果与预期偏离了23.815个单位。如此小的数值其实很难去估计，事实上通过我的统计软件计算得出其对应的概率接近于0。换句话说这个实验结果几乎不可能发生。

出现这个结果的原因或者是这个牌手夸大了或者编造了实验数据，或者在统计数据时犯了一个常见的错误：忽略了一些AK战胜AQ的样本（因为这是“理所当然”的）。这是一个被称为“感知偏离的”心理现象：我们总是会倾向于记住一些不常见的事情，而忽略一些我们认为应该发生的事情。或者我们所打的线上网站是存在作弊的。当这个结果被邮寄过来时，我们对其反应是扑克的高波动性，以及2000手牌的样本可能出现的很宽的输出结果范围。然而，这确实使得2000手牌的输出结果（有很高的方差）与一手牌（有小的多的方差）的输出结果之间产生了一些复杂的不同点。而单手牌输赢bb数的方差又远高于翻牌前双方全下的输赢次数的方差。因此，这个事件给我们的启发就是不要对扑克中产生的这种高波动事件反应太激烈，相比一些其他低波动性的事件的话。

我们打扑克时会发生很多随机的事件。我们与桌子上的其他牌手都是被随机地发到牌，其分布是所有两张牌的随机组合。一些下注，或者发出的公共牌都会改变我们手上牌的价值。而每手牌都会给我们带来收益，或者是赢下一个大底池，或者偷到盲注，或者损失一两个盲，或者输掉一个大底池。这些输出结果被一些随机的微小事件所影响，但也会被一些非随机的事件所影响：比如你对你的对手有一个阅读，可以帮助你做出一个正确的跟注或者正确的弃牌。总之，中心极限定理的力量就是把我们单手牌的输出结果组合在一起，成为一个分布，尽管他们都是随机变量。同样的，我们一个session、一周、一个月甚至整个扑克生涯的牌局记录，只要达到了一定的数量，都可以归结为这样一个分布。

标准差的平方根关系在这里就有特别的用处了，因为它使得输出结果偏离预期均值太多的可能性程度不会随着手牌数量的增加而增加。

假设我们现在与一个牌手的样本结果，他每百手牌盈利75刀，并且每手牌的方差为6400刀。我们对其不同手牌数量的样本进行估计，会发现样本的数量如何影响估计的结果。我们首先假定预估的区间为95.5%，也就是说一个牌手的盈利结果95.5%的可能性会落在这个区间内，表格如图：

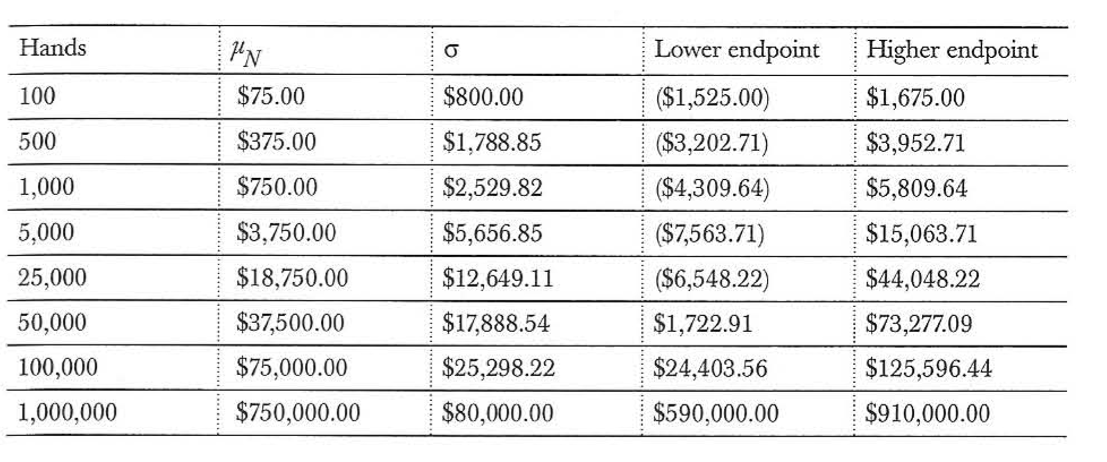
这里Lowerendpoint是下区间，Higherendpoint是上区间，带括号的是负数。

从这个表格我们可以看出，当样本数量很少时，这个选手是否盈利是不好说的。但是，随着样本数量的增加，样本数据与其本身数据的相关性也在增加（尽管取值范围的区间也增加了）。比较100万手牌与100手牌，前者的标准差是后者的100倍，但手牌数量增加了1万倍，两者差距相当大。这就是大数定律的力量：样本越大，样本的偏离预期程度就越小。

（本章完）