《The Mathematics of Poker》中文翻译

一个典型的贝叶斯定理的例子来自于医疗领域。假设我们有一个对特定疫情的筛选过程。如果某一个有疫情的个体被扫描到了，那么这个个体有80%的可能性被检测到。如果一个没有疫情的个体被扫描到了，那么这个个体有10%的可能性被误检测到。总体中有5%的个体有疫情（平均来说）。

假设一个从总体中随机选择到的人，经检测发现结果是有疫情。那么这个人真的有疫情的概率是多少呢？（不经过后续检验的情况下）

如果你回答“80%左右，或者略少于80%”，那么你就错了，但不止你一个人是这么想的。一些医生对这个问题的答案显示了也许对贝叶斯定理理解的严重不足。

我们可以通过贝叶斯定理如下解决这个问题：

A=检验过程检测为有疫情。

B=这个病人真的有疫情。

之后我们要求出P(A|B)的概率并且有以下事实：

P(A|B)=0.8

（如果这个病人有疫情，那么他有80%的机会被检测到）

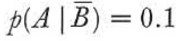
(如果这个病人没有疫情，那么他又10%的机会被误检测到）

P(B)=0.05（所有人中有5%的有疫情）

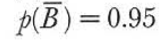
之后利用贝叶斯定理，我们有

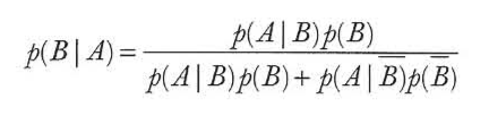
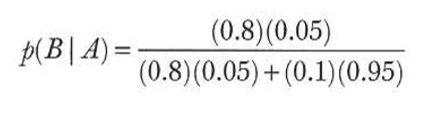
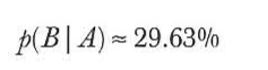
像你所看到的这样，一个被检测为有疫情并且他真的有疫情的概率远低于80%，也就是这个检测所给出的可以检测出一个人疫情的“准确率”。测试这个检验过程必须在之后增加其他的程序来确认疫情出现的情况。