《The Mathematics of Poker》中文翻译

但相比只是讨论数学等式，我们不如来考虑一下一个100000人的总体样本，在这个检验过程中会发生些什么吧。

对于这100000个人来说：

有5000人确实有疫情。（总体的5%）

有95000人没有疫情。（总体的95%）

对于其中5000个确实有疫情的人来说：

4000人会被检测出有疫情。（80%）

1000人会被遗漏。（20%）

对于其中95000个没有疫情的人来说：

9500人会被误检测为有疫情（10%）

85500会被检测为健康（90%）

现在我们的问题变成了：如果一个人被检测为有疫情，那么他有多少的概率是真的患病了呢？总共100000个样本中，有13500人被检测为有疫情。而这些人中，有4000人是真的患病了。

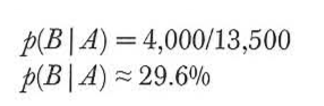
另外，我们可以看出，随着检验精度的增加，不管是使得检验出真实患病病人的准确率提高，还是降低误检测健康病人有疫情的概率，我们都可以增加检测为有疫情的人确实患病这一条件概率。注意这并没有增加一个人患病的概率——我们当然不想增加一个人患病的概率！——但是我们减少了健康的人被误检测为由疫情的概率，而这可能会引起那些原本没有疫情的人的紧张的情绪。

假设我们增加了检测出真实有疫情的人的效率，而误检测没有疫情的人的概率不变。那么通过贝叶斯定理：

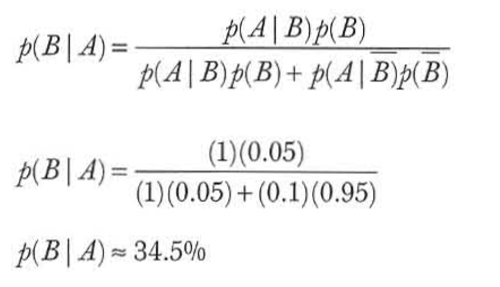
类似地，如果我们保持检测出真实有疫情的概率80%不变，而把误检测为有疫情的概率从10%降低到6%，那么我们有：

贝叶斯定理应用的关键是先验概率的存在和新的信息的收集。在上面这个例子中，我们是从有5%的人有疫情这个先验概率出发的。经过检验后，积极的结果是我们可以重新审视“病人”患病的概率——在这个例子中概率是增加了。这个过程被称为贝叶斯推断，并且对成功的扑克玩法是相当重要的。